서로소 집합(Disjoint-sets)

1. 서로소 집합의 개념 및 이해 🛺

1. 개념

• 서로소 집합이란 서로 중복 포함된 원소가 없는 집합을 말한다.
• 교집합이 없는(null) 집합이다.

2. 대표자

• 집합에 속한 하나의 특정 멤버를 대표자라고 한다.
• 이는 집합을 구분하기 위해 사용된다.

3. 예시

  빠른 이해를 위해 간단한 예시를 살펴보자. 5명의 학생(A, B, C, D, E)이 있다고 하자.

{A}, {B}, {C}, {D}, {E}

  아래와 같은 친구 관계가 있다고 하자.

A - B
B - C
D - E

  친구 관계를 통해서 2개의 집합을 만들 수 있다.

G1 = {A, B, C}
G2 = {D, E}

  서로 중복 포함된 원소가 없으므로 이는 서로소 집합이다. (한 사람이 분신술을 써서 양쪽 집합에 포함될 수 없으므로 당연한 결과이다.)

 

2. 표현 방법 2가지 🚜

1. Linked list (연결 리스트)

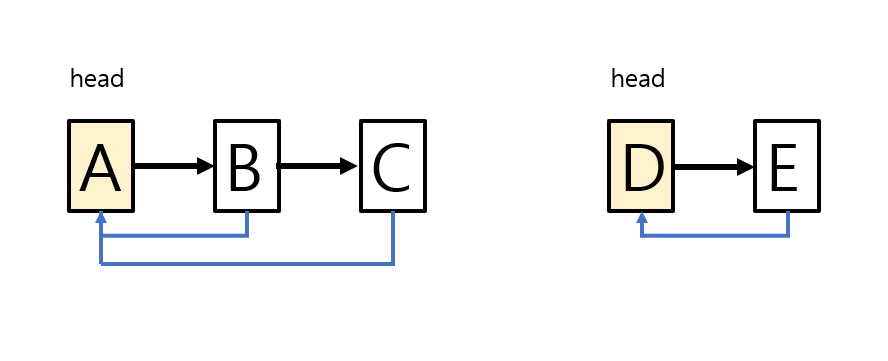
• 같은 집합의 원소들은 하나의 연결리스트로 관리된다.
• 각 리스트의 헤드(head) 부분이 해당 집합의 대표자이다.
• 노드에 헤드를 가리키는 포인터를 포함시킨다. (이전 원소를 가리키는 게 아닌 바로 헤드를 가리키는 이유는 뒤에서 나오는 Path Compression의 방법을 보면 이해할 수 있다.)

2. Tree (트리)

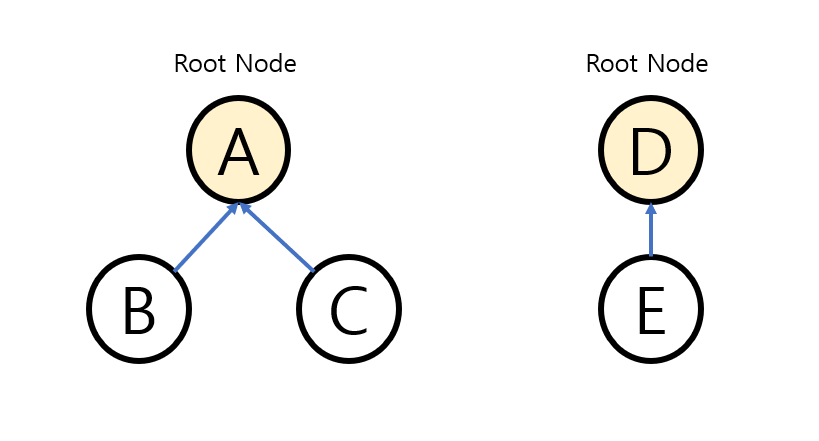
• 두 개의 요소가 같은 트리에 존재한다면 같은 집합을 의미한다.
• 루트 노드가 대표자가 된다.
  (친구관계의 예시에서 B와 C를 연결하는 과정에서 C가 A에 붙은 이유는 뒤에 나오는 내용을 보면 이해가 가능하다.)

 

3. 연산 3가지 🚙

  배열로 표현한 트리를 이용하여 살펴보자. 아래 두 가지를 잘 기억하면서 진행해보자.

1. 대표자는 자신을 가리킨다. 
   parents[i] = i
2. 자신을 가리키지 않으면 트리를 타고 올라가면서 대표자를 찾을 수 있다. 

1. makeSet()

  자기 자신이 대표자로 하는 배열을 생성한다.

static void makeSet() {

    parents = new int[N];

    for(int i = 0; i < N; i++) {
        parents[i] = i;
    }
}

2. findSet(a)

  a를 포함하는 집합의 대표자를 찾는다.

static int findSet(int a) {

    if(parents[a] == a) {
        return a;
    }
    else {
        return findSet(parents[a]);
    }
}

3. union(a, b)

  a와 b를 포함하는 두 집합을 통합한다.

static void union(int a, int b) {
    int aRoot = findSet(a);
    int bRoot = findSet(b);

    // 이미 같은 집합인 경우
    if(aRoot == bRoot) {
        return;
    }

    parents[bRoot] = aRoot;
}

 

4. 개선점 🚛

  대표자를 찾기 위해 find를 사용하는 경우, 트리의 하단부에 있을수록 더 많은 탐색이 요구된다.(노드를 타고 계속 올라가야 한다.) 즉, 트리의 높이에 영향을 많이 받게 된다.
  트리의 높이를 줄이기 위해(효율성을 증가시키기 위해) 'Path Compression'과 'Union By Rank'를 사용할 수 있다.

1. Path Compression

  이 방법은 대표자를 찾기 위해 트리를 타고 올라가도록 설계하는 것이 아닌 바로 대표자를 가리키도록 설계하는 것이다.
이는 find메서드에서 쉽게 구현할 수 있다.

static int findSet(int a) {

    if(parents[a] == a) {
        return a;
    }
    else {
        // 기존
        // return findSet(parents[a]);

        // 변경 (Path Compression)
        return parents[a] = findSet(parents[a]);   
    }
}

2. Union By Rank

  Union By Rank를 사용하기 위해서 rank[]라는 새로운 배열이 필요하다. rank[i]는 i를 루트로 하는 서브트리의 높이다. 두 집합을 합칠 때 rank가 낮은 집합이 rank가 높은 집합 아래로 들어가게 된다.

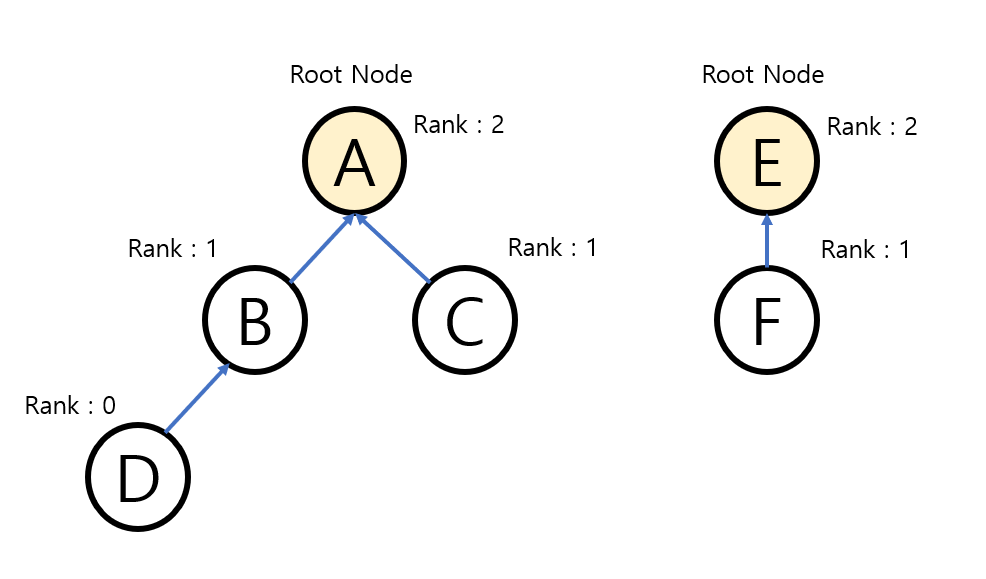
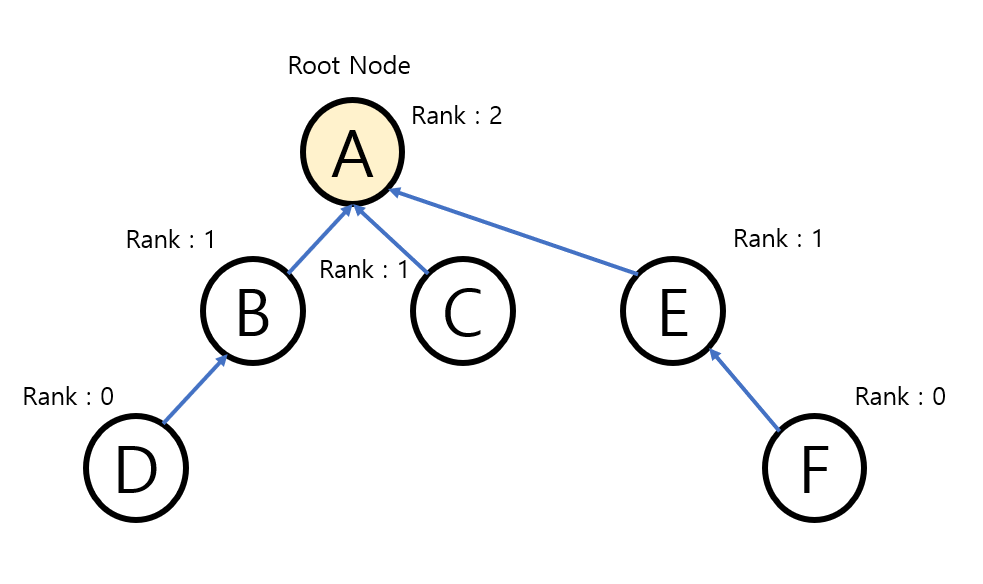
static void union(int a, int b) {
    int aRoot = findSet(a);
    int bRoot = findSet(b);

    // 같은 집합인 경우
    if(aRoot == bRoot) {
        return;
    }

    int aRank = rank[aRoot];
    int bRank = rank[bRoot];

    if(aRank < bRank) {
        parents[aRank] = bRank;
    }
    else if(aRank > bRank) {
        parents[bRank] = aRank;
    }
    else {
        parents[aRank] = bRank;
        rank[aRank]++;

        // 순서를 바꿔도 상관없음
        // parents[bRank] = aRank; 
        // rank[bRank]++;
    }
}

 

5. 시간복잡도 & 공간복잡도 🚎

1. 시간복잡도

• makeSet을 이용하여 n개의 원소로 집합을 생성하는 데 걸리는 시간 : O(n)
• findSet 또는 union을 사용하는 데 걸리는 시간 : O(log n)

  ⇒  전체 시간 복잡도 : O(n + log n)

2. 공간복잡도

n개의 요소를 저장하므로 O(n)

 

 

---

[참고자료]

Disjoint Set Data Structures - GeeksforGeeks